We are tackling various problems in information communication, machine learning, etc. using the notions and techniques of statistical mechanics. However, unlike mechanics and electromagnetics, there are few occasions where one encounters the notions of statistical mechanics before formally studying it. This may make it difficult to imagine the research conducted by our group. Here, we would like to introduce our elemental idea in a non-technical manner.
Bridging the "micro" and "macro"
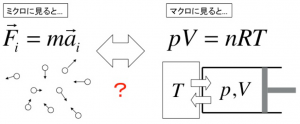
As a simple example, let us consider ideal gases. In high school physics courses, we learn that ideal gases obey the “equation of state” \(pV =nRT\), where \(p\), \(V\), \(n\), \(R\), and \(T\) denote pressure, volume of container, mole number, gas constant, and absolute temperature, respectively. Today, we almost doubtlessly accept that gases are composed of many gas molecules. We also learn that each gas molecule obeys the “equation of motion” \(\vec{F}=m\vec{a}\) (or Schrödinger equation in the case of quantum theory). These indicate that there are two different equations governing the same system depending on the scale we focus on. Then, how can these equations be compatible? Statistical mechanics addresses such questions.
More is different
We mentioned that gases are composed of gas molecules. However, such hierarchic structures are not limited to gases, and similar structures can be found in almost everything. This can be roughly expressed as
Elemental particles→Atoms→Molecules→Cells→Biological tissues→Biological bodies→Communities→....
At every level, systems are composed of the elements just below in the hierarchy. Then, can we understand everything if the ultimate governing rule of the lowest hierarchy, namely, the elemental particles, is discovered? This is a divisive subject, but perhaps, we cannot. This is because statistical mechanics implies that phenomena that is unpredictable by the theory of one hierarchy can be understood when we focus on the hierarchy just above it. Such limitations of the predictability of theories between different hierarchies are sometimes called “More is different.”
Slogan of our group is "More is different in information science as well"
Scientific approaches that try to understand phenomena by reducing them to other simpler or more fundamental phenomena are termed “reductionism.” It is based on the belief that one should be able to understand all phenomena in higher hierarchies if the theories in lower hierarchies are understood. From this viewpoint, “more is different” leads to a negative conclusion. However, this may not always be the case as it implies that qualitatively different governing rules can be compatible between different hierarchies. For instance, in information science, we encounter many combinatorial problems, which are computationally difficult to solve. However, sometimes changing the description hierarchy by considering problem ensembles, taking the large system limit, etc. can provide us with new insights and/or solution methods that we could not find by directly solving the original problems. The main interest of our group is to deepen and advance such approaches in information science.