我々の研究室では,統計力学という物理の考え方にもとづいて情報通信や機械学習など情報科学に現われるさまざまな問題に取り組んでいます.とは言っても,力学や電磁気学とは 違って,中学,高校,大学の教養科目で習う物理の授業では統計力学の考え方はあまり出てきません.そのため,統計力学を情報科学の問題に応用すると言っても,それだけでは皆さんにうまく伝わらないかもしれません.以下では,あまり専門的にならないように少し引いた視点から我々の研究について紹介したいと思います.
ミクロとマクロをつなぐ
簡単な例として,気体について考えてみましょう.高校でも習いますが,理想気体では圧力を\(p\),体積を\(V\),絶対温度を\(T\)とすると平衡状態において\(pV =nRT\)という関係式が成り立ちます( \(n, R\) はそれぞれ物質量,気体定数).現代人である我々は気体が分子という小さな粒子の集合体であることをほぼ疑いなく受け入れています.ところで,集合体ではなくその構成要素である気体分子に目を向けると,古典系ではそれらは\(\vec{F}=m\vec{a}\)という運動方程式に従うはずです(量子系ではシュレデ ィンガー方程式).同じものを見ているのに,これでは見方によって対象を支配する方程式が異なってしまうことになります.これら2つの方程式がどうやって矛盾なく両立しているのか?こうした問題に取り組んでいるのが統計力学です.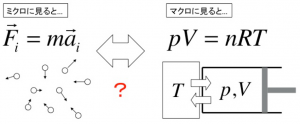
More is different(量は質を変える)
気体は気体分子の集合体と書きましたが,こうした見方はほとんどすべての物事に当てはまります.物質の究極の構成要素は素粒子ですが,それらがどのように集まって我々の社会ができているかを大雑把に表現してみると
素粒子→原子→分子→細胞→生体組織→生体→社会→...
といった階層性があることがわかります.では,一番左に位置する素粒子の支配法 則が解き明かされれば右側に位置するすべての物事がわかるようになるのでしょうか?ここは意見が分かれるポイントですが,おそらく不可能でしょう.なぜなら,階層が一つ上がる毎に下の階層の理論では予想もつかない現象が上の階層で生じ 得ることを統計力学の考察は示しているからです.このことはしばしば More is different(量は質を変える)と表現されます.
我々の研究=情報の世界でも More is different
物事をその構成要素に分解して理解しようとする科学の方法は還元論とよばれ ます.還元論の根底には階層性の連関の中で下部の理論さえ構築できれば上部のことはわかる(はず)とする考えがあります.こうした観点からすると More is different は否定的な結論です.でも悪いことばかりではありません.More is different は階層毎に質の異なる法則が成り立ってもよい,ということを示唆しているからです.たとえば,情報科学では組み合わせ問題が沢山現れますが,それらをそのまま解いたり分析したりすることは,しばしば,絶望的に難しい作業になります.ところが,問題のアンサンブルや問題サイズを無限に大きくした極限を考えると,記述の階層が変わることにより,そのまま解いた場合にはわからなかった問題の性質や解き方が見えてくることがあります.我々の研究室ではもっぱらこうし た研究を行っています.